18,039 views

Transformer Ratings
Transformer size or capacity is most often expressed in kVA. “We require 30 kVA of power for this system” is one example, or “The facility has a 480 VAC feed rated for 112.5 kVA”.
However, reliance upon only kVA rating can result insafety and performance problems when sizing transformers to feed modern electronic equipment.
Use of off-the-shelf, general purpose transformers for electronics loads can lead to power quality and siting problems:
- Single phase electronic loads can cause excessive transformer heating.
- Electronic loads draw non-linear currents, resulting in low voltage and output voltage distortion.
- Oversizing for impedance and thermal performance can result in a transformer with a significantly larger footprint.
It is vital for the systems designer to understand all of the factors that affect transformer effectiveness and performance.
.
Thermal Performance
Historically, transformers have been developed to supply 60 Hz, linear loads such as lights, motors, and heaters. Electronic loads were a small part of the total connected load. A system designer could be assured that if transformer voltage and current ratings were not exceeded, the transformer would not overheat, and would perform as expected. A standard transformer is designed and specified with three main parameters: kVA Rating, Impedance, and Temperature Rise.
.
KVA Rating
The transformer voltage and current specification. KVA is simply the load voltage times the load current. A single phase transformer rated for 120 VAC and 20 Amperes would be rated for 120 x 20 = 2400 VA, or 2.4 KVA (thousand VA).
.
Impedance
Transformer Impedance and Voltage Regulation are closely related: a measure of the transformer voltage drop when supplying full load current. A transformer with a nominal output voltage of 120 VAC and a Voltage Regulation of 5% has an output voltage of 120 VAC at no-load and (120 VAC – 5%) at full load – the transformer output voltage will be 114 VAC at full load. Impedance is related to the transformer thermal performance because any voltage drop in the transformer is converted to heat in the windings.
.
Temperature Rise
Steel selection, winding capacity, impedance, leakage current, overall steel and winding design contribute to total transformer heat loss. The transformer heat loss causes the transformer temperature to rise. Manufacturers design the transformer cooling, and select materials, to accommodate this temperature rise.
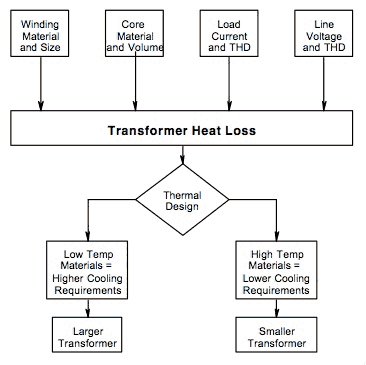
Transformer Heat Loss
Use of less expensive material with a lower temperature rating will require the manufacturer to design the transformer for higher airflow and cooling, often resulting in a larger transformer. Use of higher quality materials with a higher temperature rating permits a more compact transformer design.
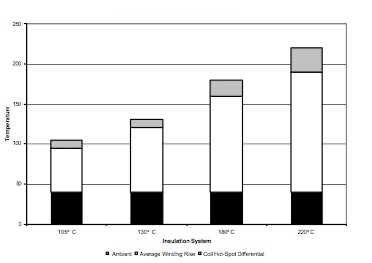
Transformer Insulation Systems
.
“K” Factor Transformer Rating
In the 1980′s, power quality engineers began encountering a new phenomenon: non-linear loads, such as computers and peripherals, began to exceed linear loads on some distribution panels. This resulted in large harmonic currents being drawn, causing excessive transformer heating due to eddy-current losses, skin effect, and core flux density increases.
Standard transformers, not designed for nonlinear harmonic currents were overheating and failing even though RMS currents were well within transformer ratings.
In response to this problem, IEEE C57.110-1986 developed a method of quantifying harmonic currents. A “k” factor was the result, calculated from the individual harmonic components and the effective heating such a harmonic would cause in a transformer. Transformer manufacturers began designing transformers that could supply harmonic currents, rated with a “k” factor. Typical “K” factor applications include:
- K-4: Electric discharge lighting, UPS with input filtering, Programmable logic controllers and solid state controls
- K-13: Telecommunications equipment, UPS systems, multi-wire receptacle circuits in schools, health-care, and production areas
- K-20: Main-frame computer loads, solid state motor drives, critical care areas of hospitals
“K” factor is a good way to assure that transformers will not overheat and fail. However, “K” factor is primarily concerned with thermal issues. Selection of a “K” factor transformer may result in power quality improvement, but this depends upon manufacturer and design.
.
Transformer Impedance
Transformer impedance is the best measure of the transformer’s ability to supply an electronic load with optimum power quality. Many power problems do not come from the utility but are internally generated from the current requirements of other loads.
While a “K” factor transformer can feed these loads and not overheat, a low impedance transformer will provide the best quality power. As an example, consider a 5% impedance transformer. When an electronic load with a 200% inrush current is turned on, a voltage sag of 10% will result. A low impedance transformer (1%) would provide only a 2% voltage sag – a substantial improvement. Transformer impedance may be specified as a percentage, or alternately, in Ohms (Ω) from Phase- Phase or Phase-Neutral.
.
High Frequency Transformer Impedance
Most transformer impedance discussions involve the 60 Hz transformer impedance. This is the power frequency, and is the main concern for voltage drops, fault calculations, and power delivery. However, nonlinear loads draw current at higher harmonics. Voltage drops occur at both 60 Hz and higher frequencies. It is common to model transformer impedance as a resistor, often expressed in ohms. In fact, a transformer behaves more like a series resistor and inductor.
The voltage drop of the resistive portion is independent of frequency, the voltage drop of the inductor is frequency dependent.
Standard Transformer impedances rise rapidly with frequency. However, devices designed specifically for use with nonlinear loads use special winding and steel lamination designs to minimize impedance at both 60 Hz and higher frequencies. As a result, the output voltage of such designs is far better quality than for standard transformers.
.
Recommendations for Transformer Sizing
System design engineers who must specify and apply transformers have several options when selecting transformers.
.
Do It Yourself Approach
With this approach, a larger than required standard transformer is specified in order to supply harmonic currents and minimize voltage drop. Transformer oversizing was considered prudent design in the days before transformer manufacturers understood harmonic loads, and remains an attractive option from a pure cost standpoint. However, such a practice today has several problems:
- A larger footprint and volume than low impedance devices specifically designed for non-linear loads
- Poor high frequency impedance
- Future loads may lead to thermal and power quality problems
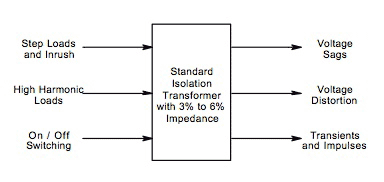
Standard Isolation Transformer
.
“K”-factor Rated Transformers
Selecting and using “K”-factor rated transformers is a prudent way to ensure that transformer overheating will not occur. Unfortunately, lack of standardization makes the “K” factor rating a measure only of thermal performance, not impedance or power quality.
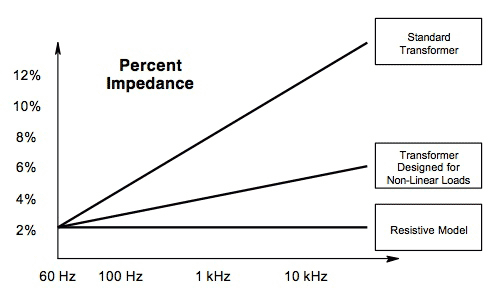
Percent Impedance
Some manufacturers achieve a good “K” factor using design techniques that lower impedance and enhance power quality, others simply derate components and temperature ratings. Only experience with a particular transformer manufacturer can determine if a “K” factor transformer addresses both thermal and power quality concerns.
.
Transformers Designed for Non-Linear Loads
Transformers designed specifically for non-linear loads incorporate substantial design improvements that address both thermal and power quality concerns. Such devices are low impedance, compact, and have better high frequency performance than standard or “K” factor designs. As a result, this type of transformer is the optimum design solution.
This type of transformer may be more expensive than standard transformers, due to higher amounts of iron and copper, higher quality materials, and more expensive winding and stacking techniques. However, the benefits of such a design in power quality and smaller size justify the extra cost, and make the low impedance transformer the most cost effective design overall.
.
Related articles
Posted by ecsanyi on Friday, June 4, 2010 at 8:24 pm
Filed under Technical Articles, Transformers · Tagged with cooling, current, high frequency, impedance, k factor, kva rating, losses, non-linear loads, power, ratings, regulation, single-phase, sizing, temperature rise, thermal performance, transformer, voltage, voltage drop
15,276 views

Busbar Technical Specification
Copper busbars are normally part of a larger generation or transmission system. The continuous rating of the main components such as generators, transformers, rectifiers, etc., therefore determine the nominal current carried by the busbars but in most power systems a one to four second short-circuit current has to be accommodated.
The value of these currents is calculated from the inductive reactances of the power system components and gives rise to different maximum short-circuit currents in the various system sections.
.
Performance under Short-circuit Conditions
Busbar trunking systems to BS EN 60439-2 are designed to withstand the effects of short-circuit currents resulting from a fault at any load point in the system, e.g. at a tap off point or at the end of a feeder run.
.
Rating under Short-circuit Conditions
The withstand ability will be expressed in one or more of the following ways:
- short-time withstand rating (current and time)
- peak current withstand rating
- conditional short-circuit rating when protected by a short-circuit protective device (s.c.p.d.)
These ratings are explained in more detail:
1. Short-time Withstand Rating
This is an expression of the value of rms current that the system can withstand for a specified period of time without being adversely affected such as to prevent further service. Typically the period of time associated with a short-circuit fault current will be 1 second, however, other time periods may be applicable.
The rated value of current may be anywhere from about 10kA up to 50kA or more according to the construction and thermal rating of the system.
2. Peak Current Withstand Rating
This defines the peak current, occurring virtually instantaneously, that the system can withstand, this being the value that exerts the maximum stress on the supporting insulation.
In an A.C. system rated in terms of short-time withstand current the peak current rating must be at least equal to the peak current produced by the natural asymmetry occurring at the initiation of a fault current in an inductive circuit. This peak is dependent on the power-factor of the circuit under fault conditions and can exceed the value of the steady state fault current by a factor of up to 2.2 times.
3. Conditional Short-circuit Rating
Short-circuit protective devices (s.c.p.ds) are commonly current-limiting devices; that is they are able to respond to a fault current within the first few milliseconds and prevent the current rising to its prospective peak value. This applies to HRC fuses and many circuit breakers in the instantaneous tripping mode. Advantage is taken of these current limiting properties in the rating of busbar trunking for high prospective fault levels. The condition is that the specified s.c.p.d. (fuse or circuit breaker) is installed up stream of the trunking. Each of the ratings above takes into account the two major effects of a fault current, these being heat and electromagnetic force.
The heating effect needs to be limited to avoid damage to supporting insulation. The electromagnetic effect produces forces between the busbars which stress the supporting mechanical structure, including vibrational forces on A.C. The only way to verify the quoted ratings satisfactorily is by means of type tests to the British Standard.
.
Type Testing
Busbar trunking systems are tested in accordance with BS EN 60439-2 to establish one or more of the short circuit withstand ratings defined above. In the case of short-time rating the specified current is applied for the quoted time. A separate test may be required to establish the peak withstand current if the quoted value is not obtained during the short-time test. In the case of a conditional rating with a specified s.c.p.d. the test is conducted with the full prospective current value at the trunking feeder unit and not less than 105% rated voltage, since the s.c.p.d. (fuse or circuit breaker) will be voltage dependent in terms of let through energy.
.
Application
It is necessary for the system designer to determine the prospective fault current at every relevant point in the installation by calculation, measurement or based on information provided e.g. by the supply authority. The method for this is well established, in general terms being the source voltage divided by the circuit impedance to each point. The designer will then select protective devices at each point where a circuit change occurs e.g. between a feeder and a distribution run of a lower current rating. The device selected must operate within the limits of the busbar trunking short-circuit withstand.
The time delay settings of any circuit breaker must be within the specified short time quoted for the prospective fault current. Any s.c.p.d. used against a conditional short-circuit rating must have energy limitation not exceeding that of the quoted s.c.p.d. For preference the s.c.p.d. recommended by the trunking manufacturer should be used.
.
Voltage Drop
The requirements for voltage-drop are given in BS 7671: Regulation 525-01-02. For busbar trunking systems the method of calculating voltage drop is given in BS EN 60439-2 from which the following guidance notes have been prepared.
Voltage Drop
Figures for voltage drop for busbar trunking systems are given in the manufacturer’s literature.
The figures are expressed in volts or milli-volts per metre or 100 metres, allowing a simple calculation for a given length of run.
The figures are usually given as line-to-line voltage drop for a 3 phase balanced load.
The figures take into account resistance to joints and temperature of conductors and assume the system is fully loaded.
Standard Data
BS EN 60439-2 requires the manufacturer to provide the following data for the purposes of calculation, where necessary:
R20 the mean ohmic resistance of the system, unloaded, at 20ºC per metre per phase
X the mean reactance of the system, per metre per phase
For systems rated over 630A:
RT the mean ohmic resistance when loaded at rated current per metre per phase
Application
In general the voltage drop figures provided by the manufacturer are used directly to establish the total voltage drop on a given system; however this will give a pessimistic result in the majority of cases.
Where a more precise calculation is required (e.g. for a very long run or where the voltage level is more critical) advantage may be taken of the basic data to obtain a more exact figure.
- Resistance – the actual current is usually lower than the rated current and hence the resistance of the conductors will be lower due to the reduced operating temperature.
.
Rx = R20 [1+0.004(Tc - 20)] ohms/metre and Tc is approximately Ta + Trwhere Rx is the actual conductor resistance
Ta is the ambient temperature
Tr is the full load temperature rise in ºC (assume say 55ºC)
- Power factor – the load power factor will influence the voltage drop according to the resistance and reactance of the busbar trunking itself.
The voltage drop line-to-line ( Δv) is calculated as follows:Δv = √ 3 I (R x cos Φ + X sin Φ) volts/metre
where I is the load current
Rx is the actual conductor resistance (Ω/m)
X is the conductor reactance (Ω/m)
Cos Φ is the load power factor
sin Φ = sin (cos-1 Φ )
- Distributed Load – where the load is tapped off the busbar trunking along its length this may also be taken into account by calculating the voltage drop for each section. As a rule of thumb the full load voltage drop may be divided by 2 to give the approximate voltage drop at the end of a system with distributed load.
. - Frequency – the manufacturers data will generally give reactance (X) at 50Hz for mains supply in the UK. At any other frequency the reactance should be re-calculated.
.
Xf = x F/50
.
where Xf is the reactance at frequency F in Hz
.
Source: Siemens Barduct Busbar Specification
.
Related articles
Posted by ecsanyi on Tuesday, March 9, 2010 at 8:00 pm
Filed under Low Voltage, Technical Articles · Tagged with busbar, busbar trunking, distributed load, en 60439-2, fault current, frequency, insulation, peak current, Power factor, reactance, resistance, rms, short circuit, type testing, voltage drop, withstand rating
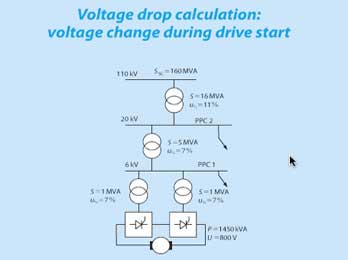
Proračun pada napona
Voltage drop is the reduction in voltage in an electrical circuit between the source and load. In electrical wiring national and local electrical codes may set guidelines for maximum voltage drop allowed in a circuit, to ensure reasonable efficiency of distribution and proper operation of electrical equipment (the maximum permitted voltage drop varies from one country to another)[1].
Voltage drop may be neglected when the impedance of the interconnecting conductors is small relative to the other components of the circuit.
.
Related articles
Posted by ecsanyi on Monday, August 10, 2009 at 12:02 am
Filed under Low Voltage, Technical Articles, Variable Speed Drives · Tagged with calculation, design engeneer, drive, voltage drop





